[알고리즘 - 그래프] 다익스트라 - 가장 먼 노드

문제

문제 링크

풀이

이 문제는 하나의 노드에서 다른 모든 노드까지의 최소 경로를 구하는 문제로 다익스트라 알고리즘을 이용해 풀이할 수 있다.

다익스트라 알고리즘

다익스트라 알고리즘은 아래와 같은 방식으로 동작한다.

1. 출발 노드 설정
2. 최단 거리 테이블 초기화
3. 방문하지 않은 && 최단 거리가 가장 짧은 노드를 선택
4. 3에서 선택한 노드를 거쳐 다른 노드로 가는 비용을 계산해 최단 거리 테이블을 갱신
5. 끝날 때 까지 3, 4번 과정을 반복

문제의 테스트 케이스에 적용

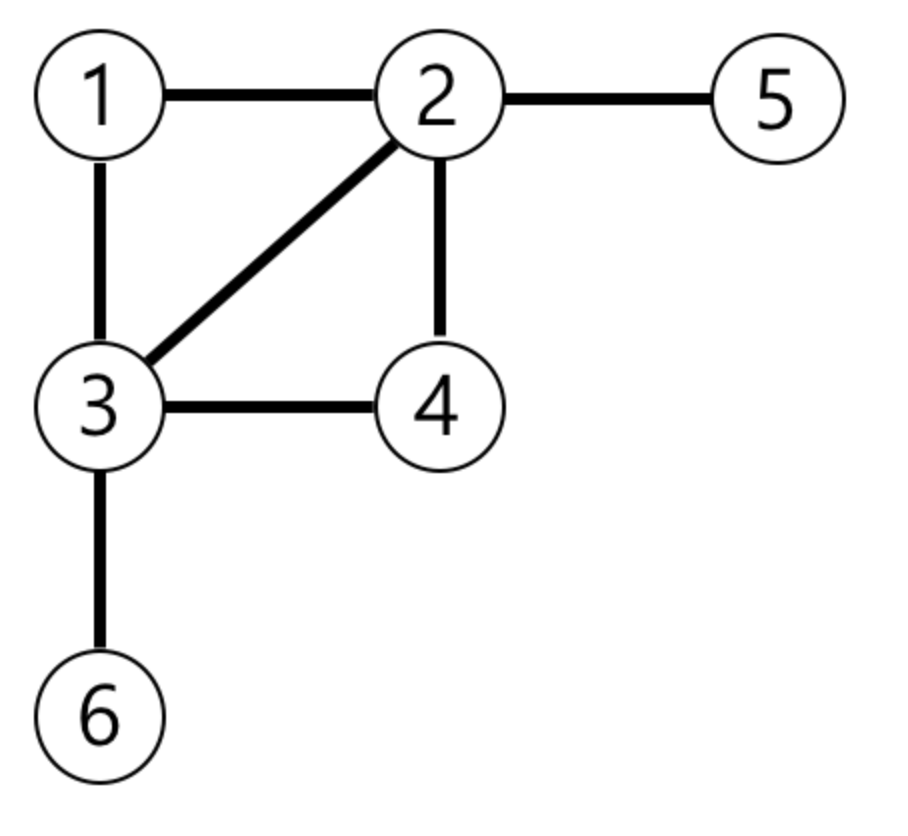
1. 1번 노드부터 나머지 노드로의 최단 경로를 구하는 문제이므로 출발 노드는 1번으로 설정
2. 간선에 가중치가 없으므로 출발노드와 이웃하는 노드까지의 거리를 1로 설정

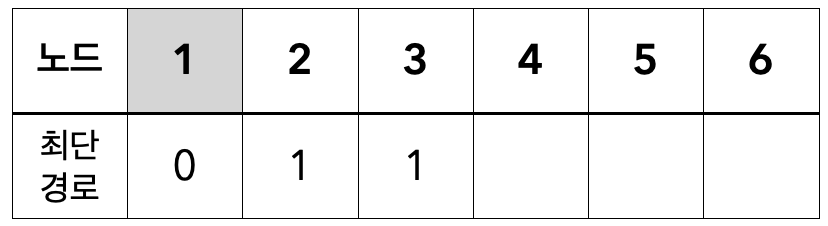
3. 방문하지 않은 노드 중 최단 경로가 최소인 2(또는 3)번 노드를 선택
4. 이웃한 노드의 최단 경로를 갱신

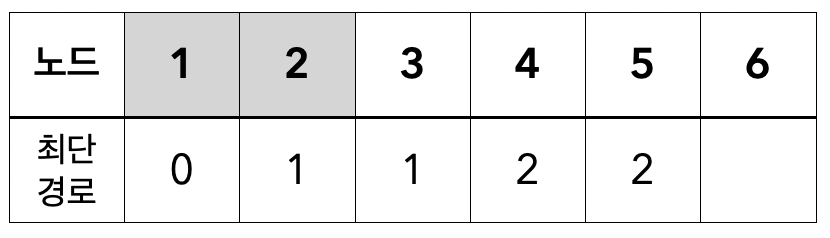
3. 방문하지 않은 노드 중 최단 경로가 최소인 3번 노드를 선택
4. 이웃한 노드의 최단 경로를 갱신

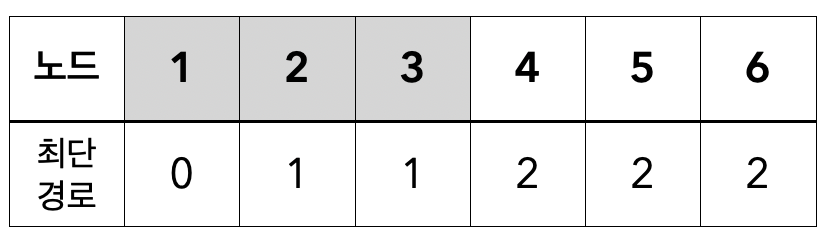
이 과정을 끝까지 반복하면 아래와 같은 상태가 된다.

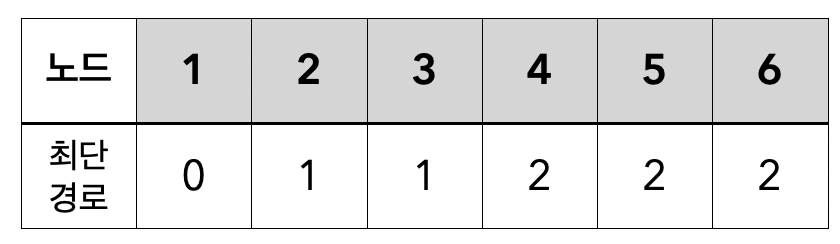
따라서 최단 경로가 최대인 노드의 개수는 3개이다.

그리디 알고리즘

다익스트라 알고리즘은 매 단계마다 최초 노드에서 경로가 최단인 노드를 선택하고 선택된 노드의 최단 경로를 그 시점에 확정하기 때문에 매 시점에 가장 최적의 해를 선택한다는 점에서 그리디 알고리즘에 속한다고 할 수 있다.

코드 (설명 포함)

import java.util.*;

class Solution {

    // 우선순위 큐에서 사용하기 위한 Node 클래스
    static class Node implements Comparable<Node>{
        int index; // 현재 노드의 index
        int currentDistance; // 현재 노드의 현재까지의 최단 경로

        Node(int index, int currentDistance) {
            this.index = index;
            this.currentDistance = currentDistance;
        }

        // 우선순위 큐에서 대소 비교를 위해 Comparable 인터페이스를 구현해야 함
        @Override
        public int compareTo(Node other) {
            return this.currentDistance - currentDistance;
        }
    }

    public int solution(int n, int[][] edge) {
        int[] distances = new int[n + 1]; // 매 시점 노드까지의 최단거리를 저장
        Arrays.fill(distances, Integer.MAX_VALUE); // 최초엔 무한(도달 불가)으로 채우기

        List<List<Integer>> graph = new ArrayList<>(); // 각 노드와 이웃한 노드 리스트를 저장

        // graph 초기화
        for (int i = 0 ; i <= n ; i++) {
            graph.add(new ArrayList<>());
        }
        // 이웃 노드 정보 추가 (양방향)
        for (int[] e : edge) {
            graph.get(e[0]).add(e[1]);
            graph.get(e[1]).add(e[0]);
        }

        // 다익스트라 알고리즘 시작

        // 매 step에 가장 최단 경로가 짧은 노드를 선택하기 위해 반복문을 도는 대신 우선순위 큐를 사용
        PriorityQueue<Node> queue = new PriorityQueue<>();
        // 초기 (1번) 노드 설정
        queue.offer(new Node(1, 0)); // Node(index, currentDistance)
        distances[1] = 0;

        while(!queue.isEmpty()) {
            Node currentNode = queue.poll();
            // 이전에 방문한 노드면 제외
            // 우선순위 큐에서 빼온 currentDistance 값이 최단 경로 테이블에 기록된 최소 경로 값보다 크면
            // 이미 방문한 노드이므로 처리할 필요 없음
            if (currentNode.currentDistance > distances[currentNode.index]) {
                continue;
            }

            // 연결된 노드들 갱신
            for (int neighbor : graph.get(currentNode.index)) {
                int newDistance = distances[currentNode.index] + 1;
                // 새로운 경로가 더 짧을 경우에만 최단 경로 테이블 갱신 및 큐에 추가
                if (newDistance < distances[neighbor]) {
                    distances[neighbor] = newDistance;
                    queue.offer(new Node(neighbor, newDistance));
                }
            }       
        }

        // 최대 경로가 몇인지 탐색
        int maxDistance = 0;
        for (int i = 1 ; i <= n ; i++) {
            maxDistance = Math.max(maxDistance, distances[i]);
        }

        // 최대 경로를 갖는 노드가 몇 개인지 탐색
        int count = 0;
        for (int distance : distances) {
            if (distance == maxDistance) {
                count++;
            }
        }
        return count;
    }
}

참고자료

• https://www.youtube.com/watch?v=acqm9mM1P6o&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC&index=7