[알고리즘 - 완전탐색] 전력망을 둘로 나누기

문제

문제 링크

풀이

문제를 푸는 여러 가지 방법이 있을 것 같았는데 간단한 방법으로 문제를 풀었다.

입력으로 간선 정보가 주어지므로 순회를 통해 하나씩 간선을 제외하고, 제외된 간선에 속한 노드를 각각 시작점으로 하여 그 시작점과 연결되어 있는 노드들의 합이 몇 개인지 카운트한다. 그리고 그렇게 카운트된 두 값의 차의 절댓값을 구한다. 이렇게 구한 절댓값의 최솟값을 계속해서 갱신해가면 모든 간선을 순회했을 때 가장 노드의 차이가 적을 때의 값을 구할 수 있다.

예를 들어 입력이 [[1,3],[2,3],[3,4],[4,5],[4,6],[4,7],[7,8],[7,9]] 라고 하면, 가장 먼저 [1, 3] 간선이 선택될 것이고 (그래프에서 해당 간선을 제외) 1번과 3번 노드를 분리해놓고 1번과 3번으로부터 시작되는 트리에 속한 노드들을 각각 구한다. 트리에 속한 노드를 구하는 방법은 여러 가지가 있겠지만 간단하게 dfs를 사용했다. 그리고 그 값의 차의 절댓값을 구하게 된다.

아래 그림은 순회를 계속하던 중 [4, 7] 간선이 제외된 상태에서의 트리이며 이 경우 6, 3이라는 값이 각각 구해지고 두 값의 차의 절댓값은 3이 나오게 된다.

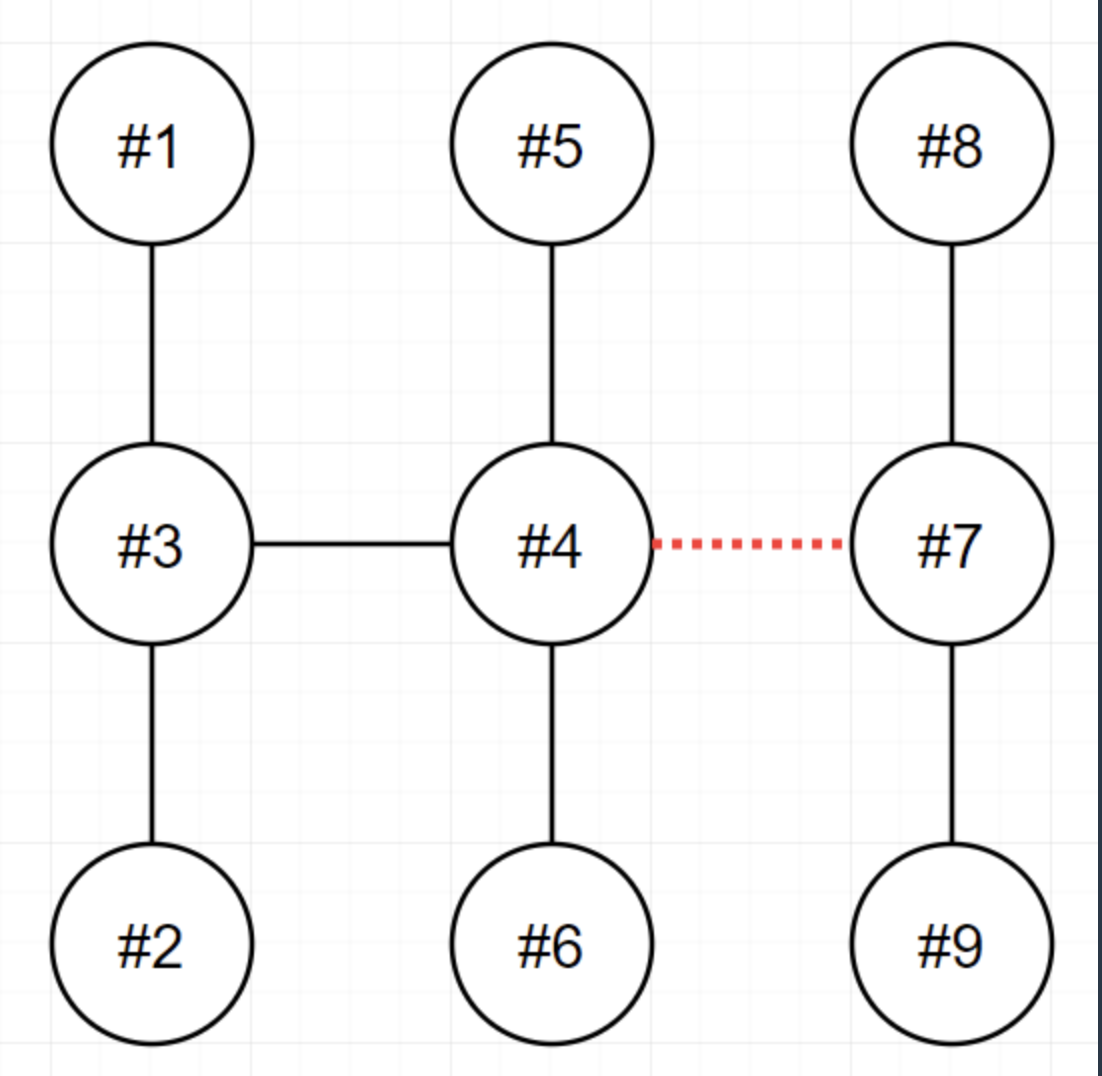
이 과정을 전체 간선에 대해 반복하면 답을 쉽게 구할 수 있다.

코드

import java.util.*;

class Solution {

    public int solution(int n, int[][] wires) {
        int answer = Integer.MAX_VALUE;

        // 전체 그래프 생성
        Map<Integer, List<Integer>> graph = new HashMap<>();
        for (int[] wire : wires) {
            int nodeA = wire[0];
            int nodeB = wire[1];

            // 양방향으로 등록
            if (graph.get(nodeA) == null) {
                graph.put(nodeA, new ArrayList<>());
            }
            graph.get(nodeA).add(nodeB);

            if (graph.get(nodeB) == null) {
                graph.put(nodeB, new ArrayList<>());
            }
            graph.get(nodeB).add(nodeA);
        }

        // 하나의 간선씩 제외하며 dfs 순회하여 최소 값 비교하기
        for (int[] wire : wires) {
            // 간선 제거
            graph.get(wire[0]).remove(Integer.valueOf(wire[1]));
            graph.get(wire[1]).remove(Integer.valueOf(wire[0]));

            // 각 노드를 시작으로 하여 각 트리의 노드 개수 확인
            int diff = dfs(n, graph, wire[0]) - dfs(n, graph, wire[1]);
            // diff의 절대값의 최소값으로 answer를 갱신
            answer = Math.min(answer, Math.abs(diff));

            // 간선 다시 추가
            graph.get(wire[0]).add(wire[1]);
            graph.get(wire[1]).add(wire[0]);
        }

        return answer;
    }

    // 노드에 연결된 노드 수를 카운트하기 위한 dfs 메서드
    public int dfs(final int n, final Map<Integer, List<Integer>> graph, int startNode) {
        int count = 0;
        Stack<Integer> stack = new Stack<>();
        boolean[] visited = new boolean[n + 1];

        stack.push(startNode);

        while(!stack.isEmpty()) {
            Integer current = stack.pop();
            count++;
            visited[current] = true;

            if (graph.get(current) == null) {
                continue;
            }

            for (Integer neighbor : graph.get(current)) {
                if (!visited[neighbor]) {
                    stack.push(neighbor);
                }
            }
        }

        return count;
    }

}