[알고리즘] graph와 탐색

비선형 자료구조

• 선형으로 표현할 수 없는 데이터를 표현할 때 사용되는 자료구조
  • 예를 들어 지하철 노선도와 같이 하나의 선으로 표현할 수 없는 데이터를 표현하고자 할 때 사용된다
• 대표적으로 graph가 비선형 구조이다

graph

• 데이터를 갖는 Node와 Node들을 이어주는 Edge로 구성
  • Edge는 단방향 / 양방향의 방향성을 가질 수 있다
  • Edge는 가중치를 가질 수 있다

데이터의 탐색

• 선형 자료구조와 달리 비선형 구조는 시작과 끝이 모호하다
• 따라서 먼저 하나의 Node를 탐색하고
  • 해당 Node와 Edge로 연결된 Node들을 탐색한다
    • 연결된 Node들은 Queue / Stack 등에 넣어 탐색을 예약해둔다
  • 원하는 Node를 찾을 때 까지 이 과정을 반복한다

탐색에 사용하는 자료구조에 따른 탐색 순서 차이

• 탐색에 Queue를 사용하면
  • 먼저 들어간 Node가 먼저 탐색되므로, 계속해서 가까운 Node로 넓게 퍼지는 형태로 Node들을 탐색한다
  • 즉, 너비 우선 탐색 (BFS, Breadth-First Search) 가 된다
• 탐색에 Stack을 사용하면
  • 더 이상 연결된 Node가 없을 때 까지 Stack 최상단 Node를 먼저 탐색하므로 가장 멀리 있는 Node를 향해 탐색하는 형태를 띈다
  • 즉, 깊이 우선 탐색 (DFS, Depth-First Search) 가 된다

코드

graph 생성

• 그래프를 표현할 수 있는 자료구조가 자바에 없으므로 직접 구현해 사용해야 한다. 자바에서 그래프를 구현할 수 있는 방법은 크게 1. 인접 리스트 와 2. 인접 행렬 이 있다
  • 인접 리스트는 각 노드가 자신과 이웃한 노드들의 리스트를 가지고 있는 방식을 말한다
    • 인접 리스트 방식에서 가중치를 표현하기 위해서는 노드에 가중치 필드를 더해주거나 가중치를 위한 별도 리스트를 만들어야 한다
  • 인접 행렬은 2차원 배열을 사용해 각 노드들이 연결되어 있는지를 표현한다. (ex. arr[3][1] == 1 이면 3번 노드에서 1번 노드로의 간선이 존재하는 식)
    • 간선에 가중치가 있는 경우 인접 행렬에 값을 넣어주는 방식으로 가중치를 표현할 수 있다

인접 리스트 예제

public class Node {
    Integer data;
    List<Node> edges = new LinkedList<>();
    boolean visited;

    public Node(int data) {
        this.data = data;
    }

    // link() 메서드를 통해 현재 노드에 이웃한 Node를 추가
    public void link(Node node) {
        this.edges.add(node);
    }

    // 양방향 연관관계 추가
    public void linkBiderectional(Node node) {
        this.link(node);
        node.link(this);
    }

    // 방문 여부 체크
    public void visit() {
        this.visited = true;
    }

    @Override
    public String toString() {
        return data.toString();
    }
}

인접 행렬 예제

• 정점이 1~N인 int형이라고 가정하면 아래와 같이 인접 행렬을 이용해 그래프를 표현할 수 있다
  • 정점이 int형이 아니라면, 정점들을 모아둔 String[] nodes 와 같은 배열을 추가로 사용해 인접 여부와 정점의 값을 별도로 저장하는 방식을 사용할 수도 있다

public class Graph {
    int[][] matrix;
    boolean[] visited;

    public Graph(int size) {
        this.matrix = new int[size + 1][size + 1];
        this.visited = new boolean[size + 1];
    }

    public void link(int vertexA, int vertexB) {
        matrix[vertexA][vertexB] = 1;
    }

    public void linkBidirectional(int vertexA, int vertexB) {
        link(vertexA, vertexB);
        link(vertexB, vertexA);
    }

    public void visit(int vertex) {
        visited[vertex] = true;
    }
}

BFS

• 맹목적인 탐색을 하고자 할 때 사용
• 최단 경로를 찾아주기 때문에, 경로가 최단거리임을 보장해야 할 때 사용 가능
  • 현재 노드에 인접한 노드를 먼저 모두 탐색하기 때문에, 최단 거리의 노드가 먼저 탐색되는 것이 보장됨

예제를 위해 아래와 같은 그래프를 사용했다.

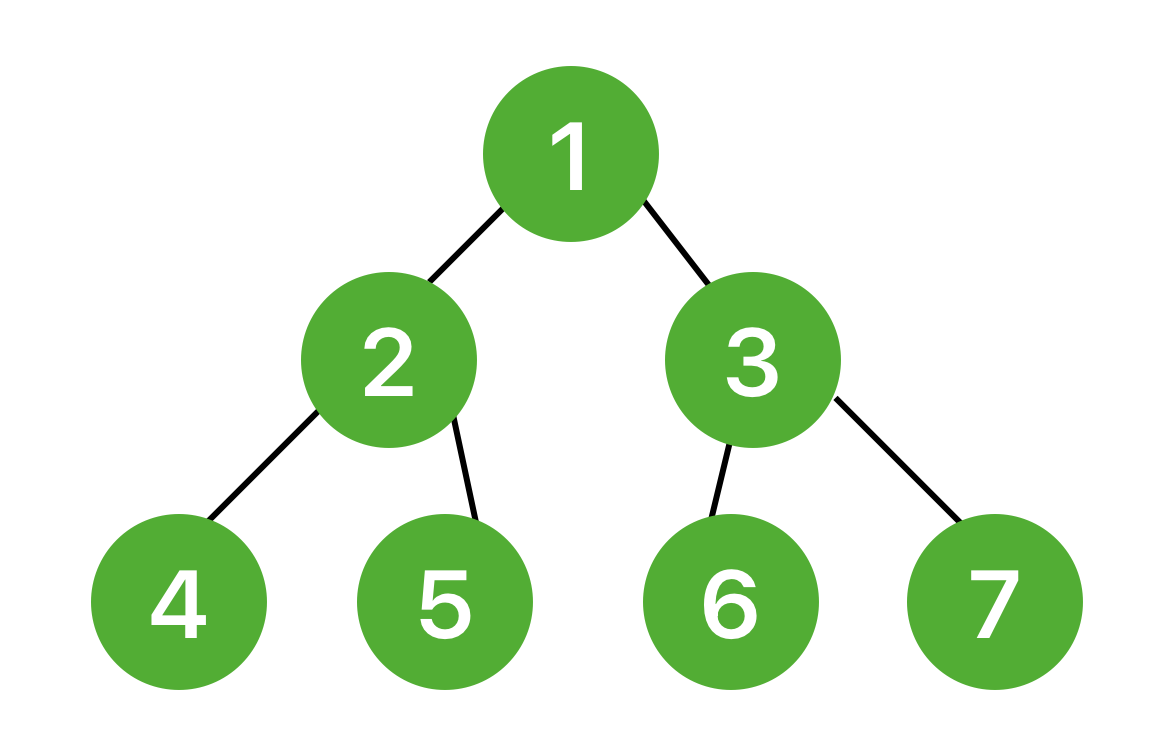
그래프는 아래와 같이 구성할 수 있다.

// graph 구성
Node node1 = new Node(1);
Node node2 = new Node(2);
Node node3 = new Node(3);
Node node4 = new Node(4);
Node node5 = new Node(5);
Node node6 = new Node(6);
Node node7 = new Node(7);

node1.linkBiderectional(node2);
node1.linkBiderectional(node3);

node2.linkBiderectional(node4);
node2.linkBiderectional(node5);

node3.linkBiderectional(node6);
node3.linkBiderectional(node7);

BFS 코드는 아래와 같다.

public static void bfs(Node head, Integer target) {
    Queue<Node> queue = new LinkedList<>();
    queue.offer(head);

    while (!queue.isEmpty()) {
        Node currentNode = queue.poll();
        // 현재 노드 방문 처리
        currentNode.visit();
        System.out.println(currentNode);

        // 타겟 여부 확인
        if (currentNode.data == target) {
            System.out.println("Target 발견 : " + currentNode.data);
            break;
        }

        // 이웃 노드 Queue에 삽입
        for (Node node : currentNode.edges) {
            if (!node.visited && !queue.contains(node)) {
                queue.offer(node);
            }
        }
    }
}

실행해보면, 아래와 같이 1 -> 2 -> 3 -> … 순으로 (너비 우선) 탐색되는 것을 볼 수 있다.

// 실행 코드
bfs(node1, 7);

// 출력
1
2
3
4
5
6
7
Target 발견 : 7

DFS

• DFS는 기본적으로 Stack을 사용해서 구현하지만, 컴퓨터가 메서드를 호출할 때 스택 프레임이 생성되므로 DFS는 재귀를 이용해도 구현할 수 있다

Stack 사용

• Stack을 사용해 DFS를 구현하는 경우, BFS 코드에서 Queue만 Stack으로 바뀌었을 뿐 나머지는 전혀 바뀌지 않는다.

public static void dfs(Node head, Integer target) {
    Stack<Node> stack = new Stack<>();
    stack.push(head);

    while (!stack.isEmpty()) {
        Node currentNode = stack.pop();
        // 현재 노드 방문 처리
        currentNode.visit();
        System.out.println(currentNode);

        // 타겟 여부 확인
        if (currentNode.data == target) {
            System.out.println("Target 발견 : " + currentNode.data);
            break;
        }

        // 이웃 노드 Stack에 삽입
        for (Node node : currentNode.edges) {
            if (!node.visited && !stack.contains(node)) {
                stack.push(node);
            }
        }
    }
}

재귀 사용

• 재귀를 사용할 경우 아래와 같이 메서드 호출이 stack push / pop 연산과 동일하게 동작한다.
  • 메서드를 호출 == Stack에 node를 push() 하는 것
  • 메서드가 호출됨 == Stack에서 node를 pop() 하는 것

public static void dfsRecursion(Node head, Integer target) {
    // 현재 노드 방문 처리
    head.visit();
    System.out.println(head);

    // 타겟 여부 확인
    if (head.data == target) {
        System.out.println("Target 발견 : " + head.data);
    }

    // 이웃 노드 호출
    for (Node node : head.edges) {
        if (!node.visited) {
            dfsRecursion(node, target);
        }
    }
}

실행해보면 BFS와 달리 깊이 우선으로 탐색되는 것을 알 수 있다.

// 실행 코드
dfsStack(node1, 7);

// 출력
1
3
7
Target 발견 : 7

// 실행 코드
dfsRecursion(node1, 7);

// 출력
1
2
4
5
3
6
7
Target 발견 : 7

레퍼런스

• https://school.programmers.co.kr/learn/courses/13577
• https://www.youtube.com/watch?v=66ZKz-FktXo&list=PLRx0vPvlEmdDHxCvAQS1_6XV4deOwfVrz&index=16&ab_channel=%EB%8F%99%EB%B9%88%EB%82%98
• https://www.youtube.com/watch?v=l0Rsu7dziws&list=PLRx0vPvlEmdDHxCvAQS1_6XV4deOwfVrz&index=17&ab_channel=%EB%8F%99%EB%B9%88%EB%82%98